Gleichverteilte Punkte in einem Kreis

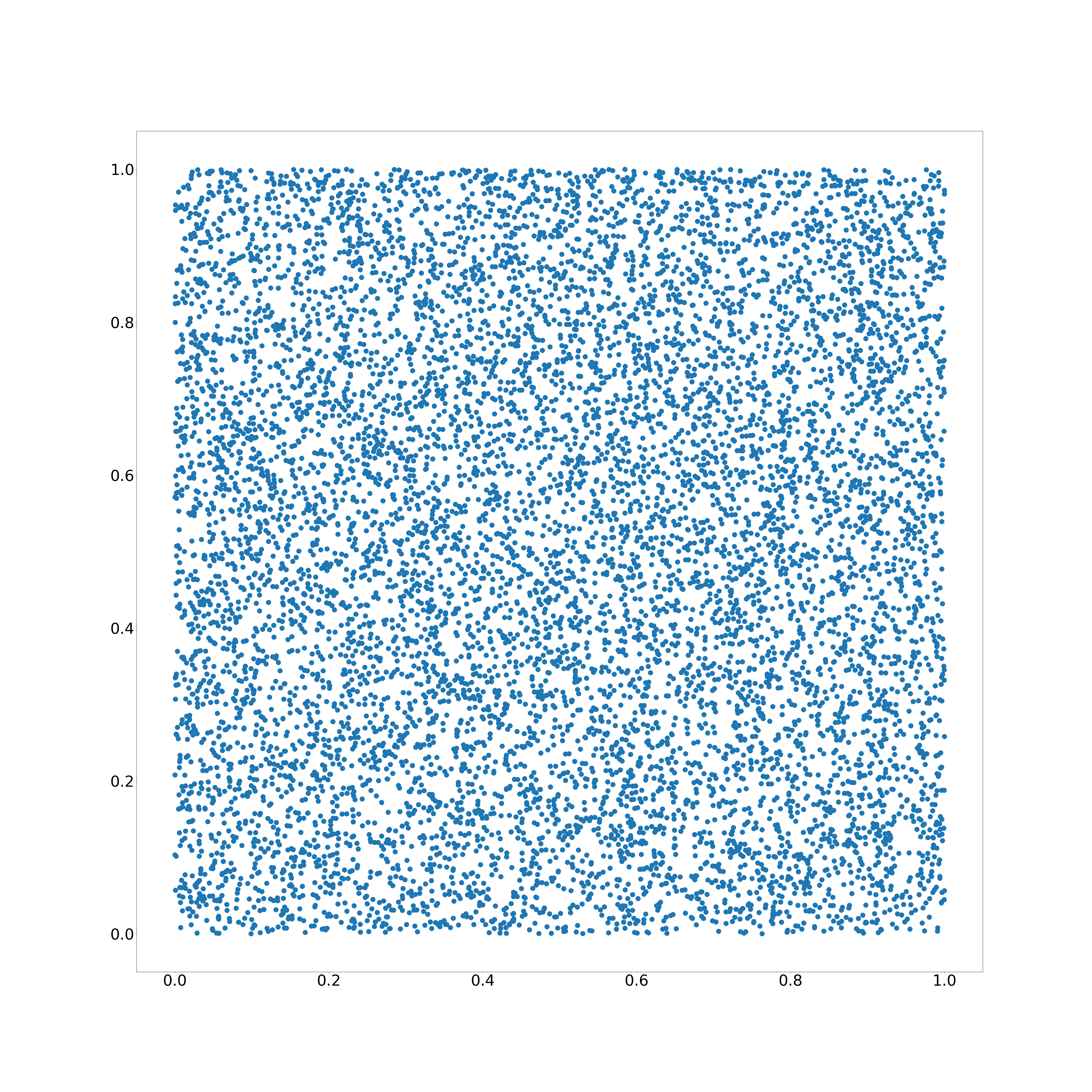
Wie bekommt man eine Gleichverteilung von Punkten in einem Kreis? Die Idee für ein Quadrat ist einfach: Man sucht sich einen zufälligen $x$-Wert und einen zufälligen $y$-Wert und erhält einen Punkt $(x, y)$.

$(x, y) = (random(), random())$

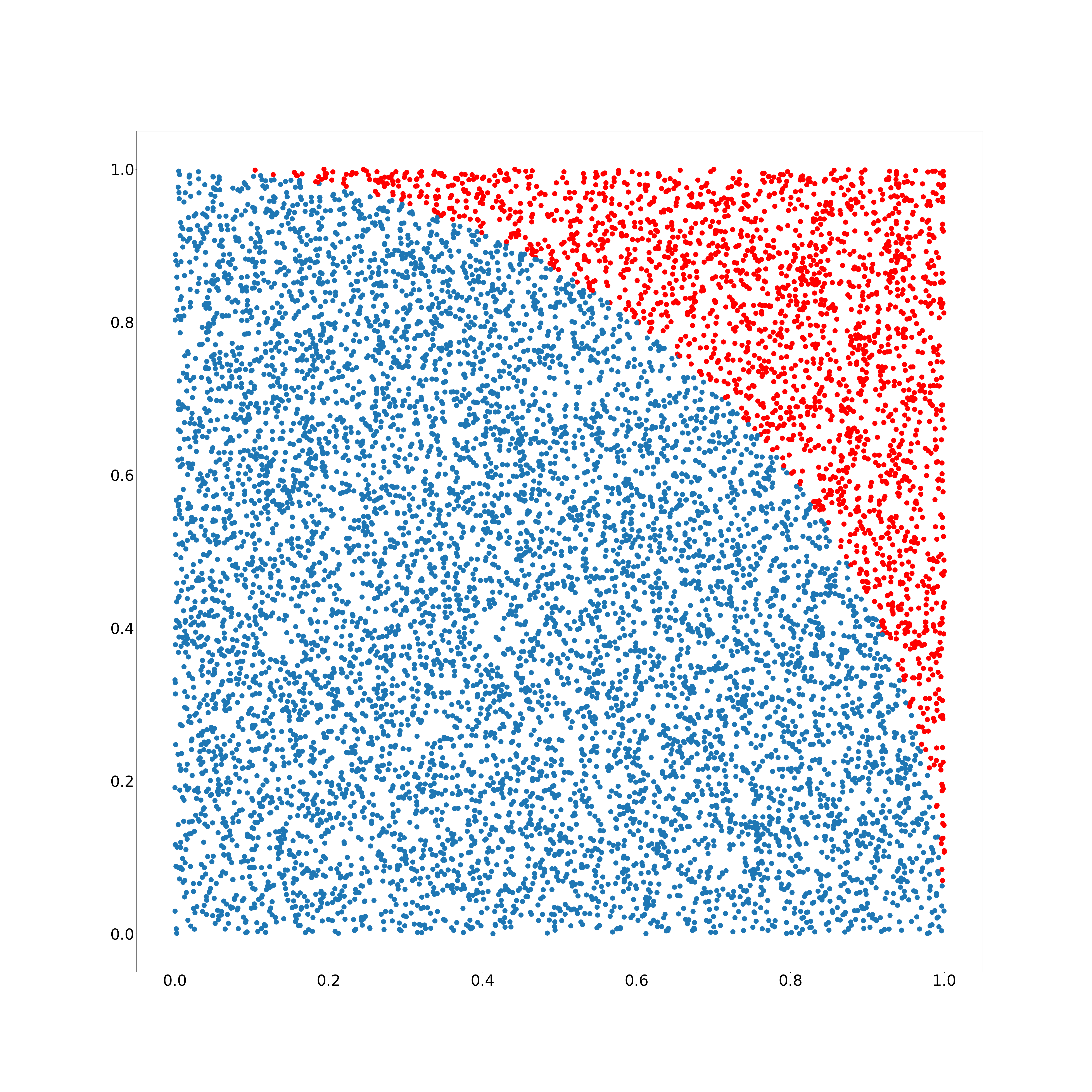
Die naive Idee einen Kreis zu erzeugen, ist, alle Punkte zu ignorieren, die außerhalb des Kreises liegen. Dafür berechnet man $ r = \sqrt{x^2 + y^2} $ und betrachtet nur die Punkte $ r \le 1 $ an.

$(x, y) = (random(), random())$, Kreis eingefärbt

Das ist aber nicht effizient. Man verliert mehr als ein Fünftel aller Punkte!

$$1 - \frac{A_{Kreis}}{A_{Quadrat}} = $$

$$ 1 - \frac{R^2\pi}{(2R)^2} = $$

$$ 1 - \frac{\pi}{4} \approx 0,2146$$

Vielleicht hilft ein anderes Koordinatensystem. Beim Polarkoordinatensystem wird ein Punkt durch einen Radius und einen Winkel $(r, \varphi)$ angegeben.

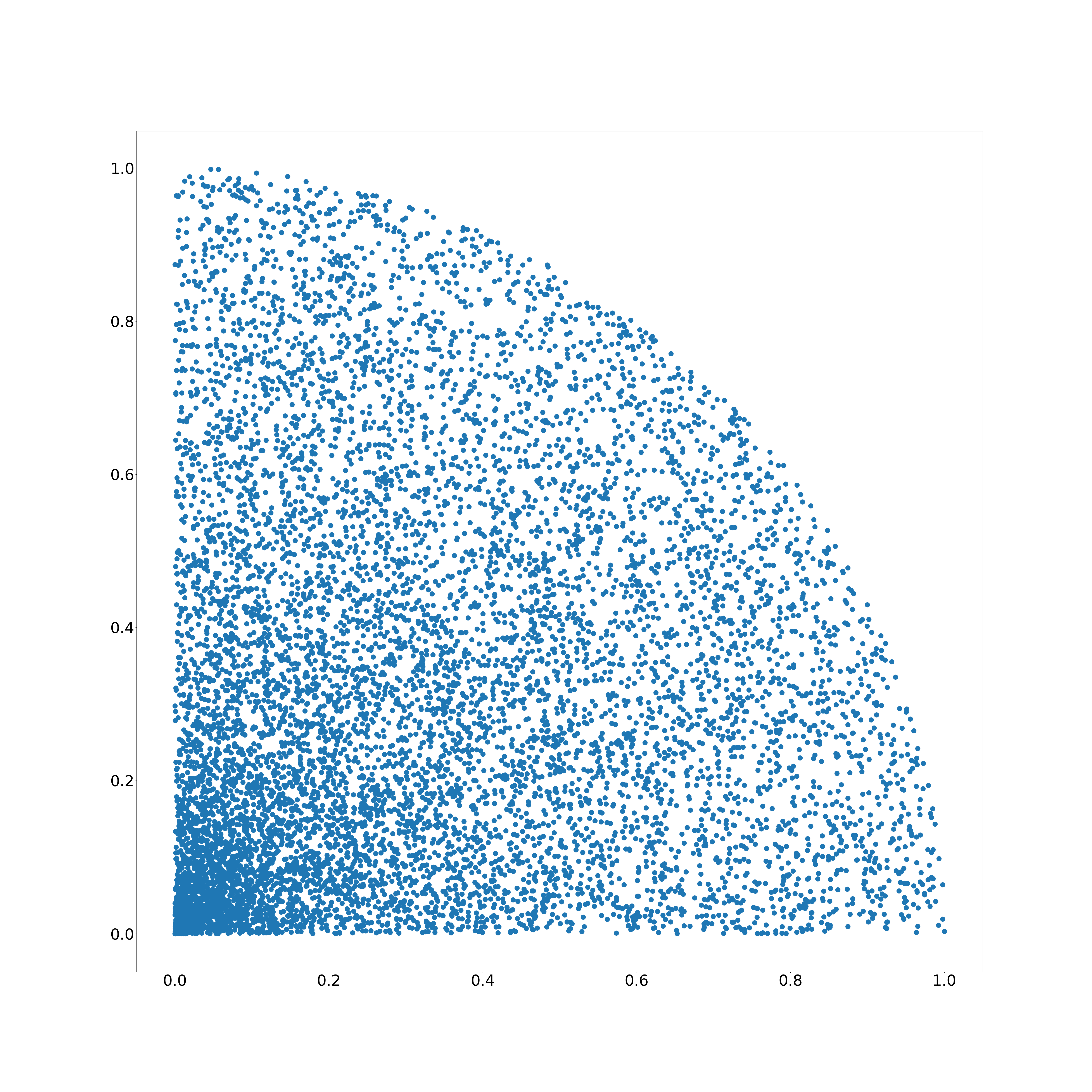
$(r, \varphi) = (random(), random() \cdot 0.5 \pi$)

Ein zufälliger Radius und ein zufälliger Winkel bilden aber keine Gleichverteilung ab.

Woran liegt das? Auf allen Strecken, die zwischen dem Mittelpunkt und dem Rand des Kreises liegen, sind gleich viele Punkte, da der Winkel ein Zufallswert ist. Ebenso liegt auf jedem Radius dieselbe Anzahl an Punkten, da der Radius ebenfalls zufällig ist.

Das Problem ist, dass ein größerer Radius einen größeren Kreis bildet. Auf einem Radius liegt aber immer dieselbe Anzahl von Punkten. Damit wird der Abstand zwischen den Punkten größer und die Dichte der Punkte nimmt mit größerem Radius ab^{[1] $$ \text{Dichte} = \frac{\text{Punkte}}{\text{Umfang}} = \frac{\text{Punkte}}{2r\pi} $$ Wird der Radius größer, wird die Dichte kleiner.} .

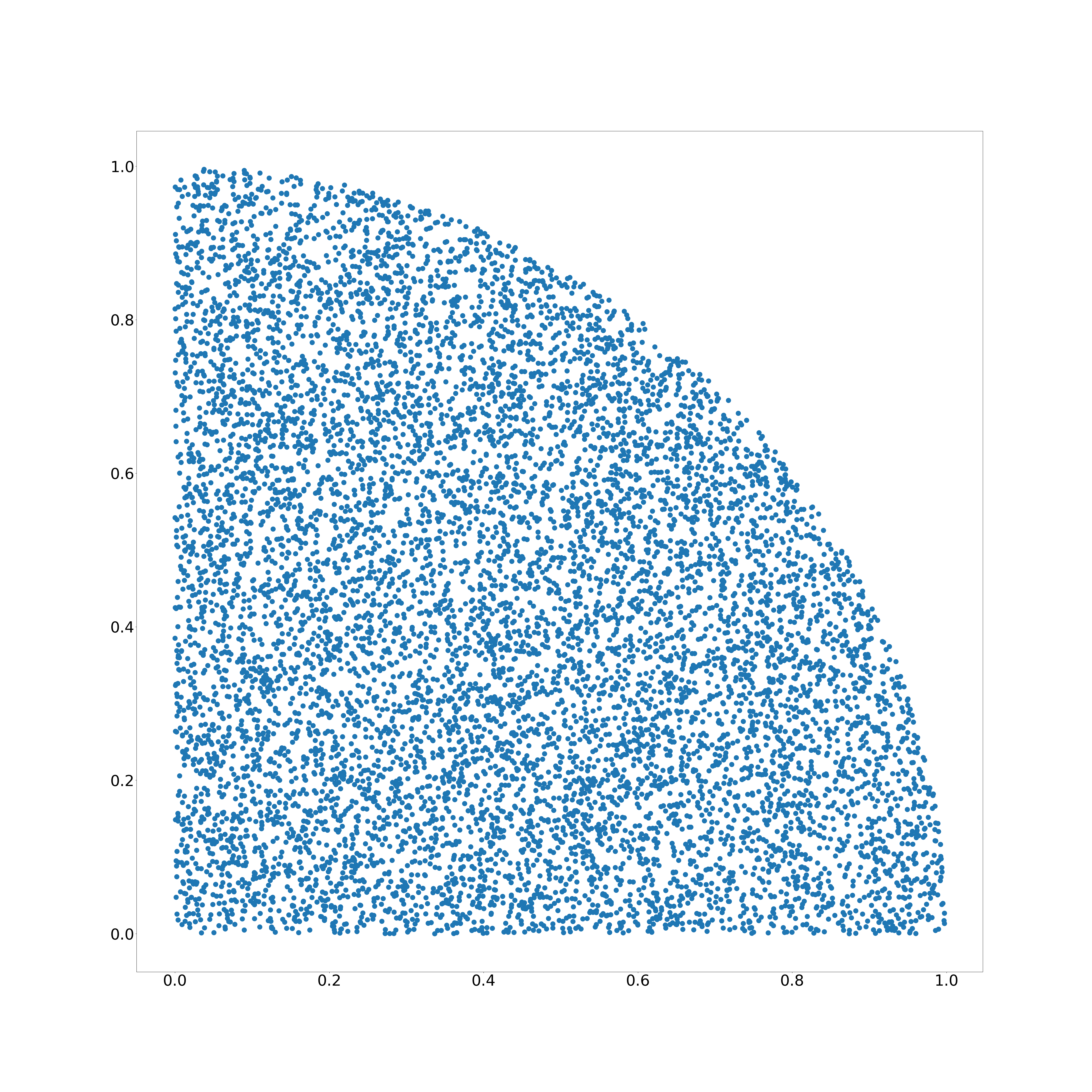
Die Lösung ist, als Radius die Wurzel einer zufälligen Zahl zu nehmen.

$(r, \varphi) = (\sqrt{random()}, random() \cdot 0,5 \pi$)

Warum funktioniert das? Mit einer Wahrscheinlichkeitsdichtefunktion (WDF) berechnet man die Wahrscheinlichkeit, einen Wert zwischen zwei Punkten zu erhalten. Bisher war unsere WDF konstant, also $f(r) = a$, da jeder Radius $r$ gleich wahrscheinlich war. In jedem gleich großen Intervall war die Anzahl der Punkte damit ebenfalls konstant.

Weil der Umfang eines Kreises aber linear wächst ($2r\pi$), brauchen wir eine WDF, die ebenfalls linear wächst und damit die Dichte (und nicht die Anzahl) der Punkte konstant hält. Die wichtigen Eigenschaften einer WDF sind, dass sie nichtnegativ ist und das Integral der Funktion von $-\infty$ bis $+\infty$ gleich $1$ ist.

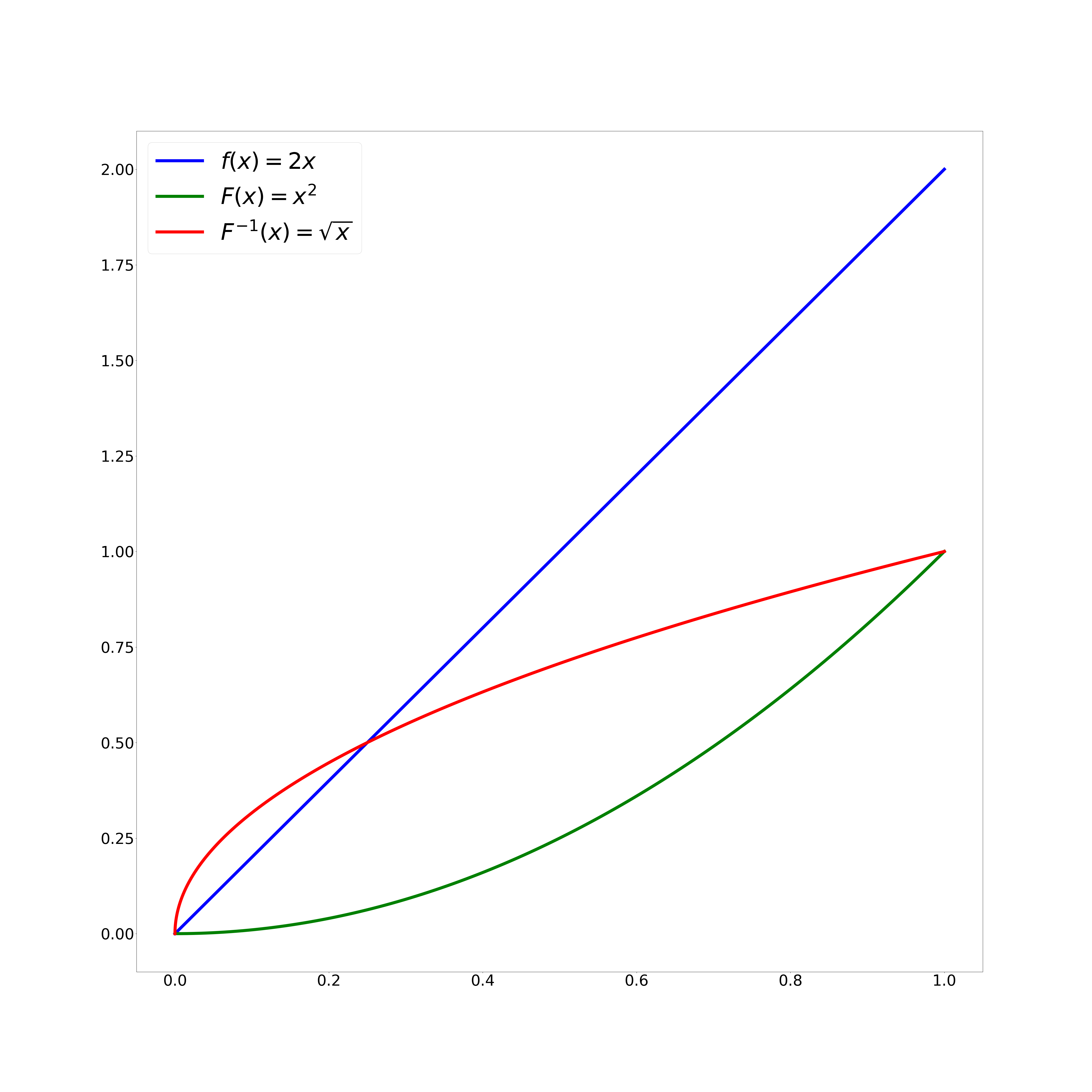
Für unser spezielles Problem wollen wir also eine lineare Funktion $f(r)$, deren Integral von 0 bis zum Kreisradius $R$ gleich $1$ ist. Die Funktion $f(r) = r$ erfüllt diese Eigenschaften nicht: $ \int_0^R f(r) dr = R^2 / 2 = 0,5$ (mit $R=1$). Die Lösung ist aber naheliegend: $f(r) = 2r/R^2$ (und damit $\int_0^R f(r) dr = R^2 = 1$).

Während die WDF die Wahrscheinlichkeitsdichte an einem bestimmten Punkt angibt, berechnet die Verteilungsfunktion die Wahrscheinlichkeit, dass ein Wert kleiner oder gleich einem gegebenen $x$ ist. Wenn wir diese Verteilungsfunktion nun umkehren, berechnet sie nicht mehr, wie wahrscheinlich ein Wert kleiner oder gleich $x$ ist, sondern gibt das größtmögliche $x$ für eine gegebene Wahrscheinlichkeit an.

Wir können diesen größtmöglichen Wert als unseren tatsächlichen Wert für den Radius wählen.

Die zugehörige Verteilungsfunktion $F(x)$ erhalten wir durch Integration:

$$ F(x) = \int_0^x f(r) dr = \frac{x^2}{R^2} $$

Die Umkehrung erhalten wir wie folgt:

$$ F^{-1}(x): x = \frac{y^2}{R^2} $$ $$ y^2 = R^2 \cdot x $$ $$ y = \sqrt{R^2 \cdot x} $$ $$ F^{-1}(x) = R \cdot \sqrt{x} $$

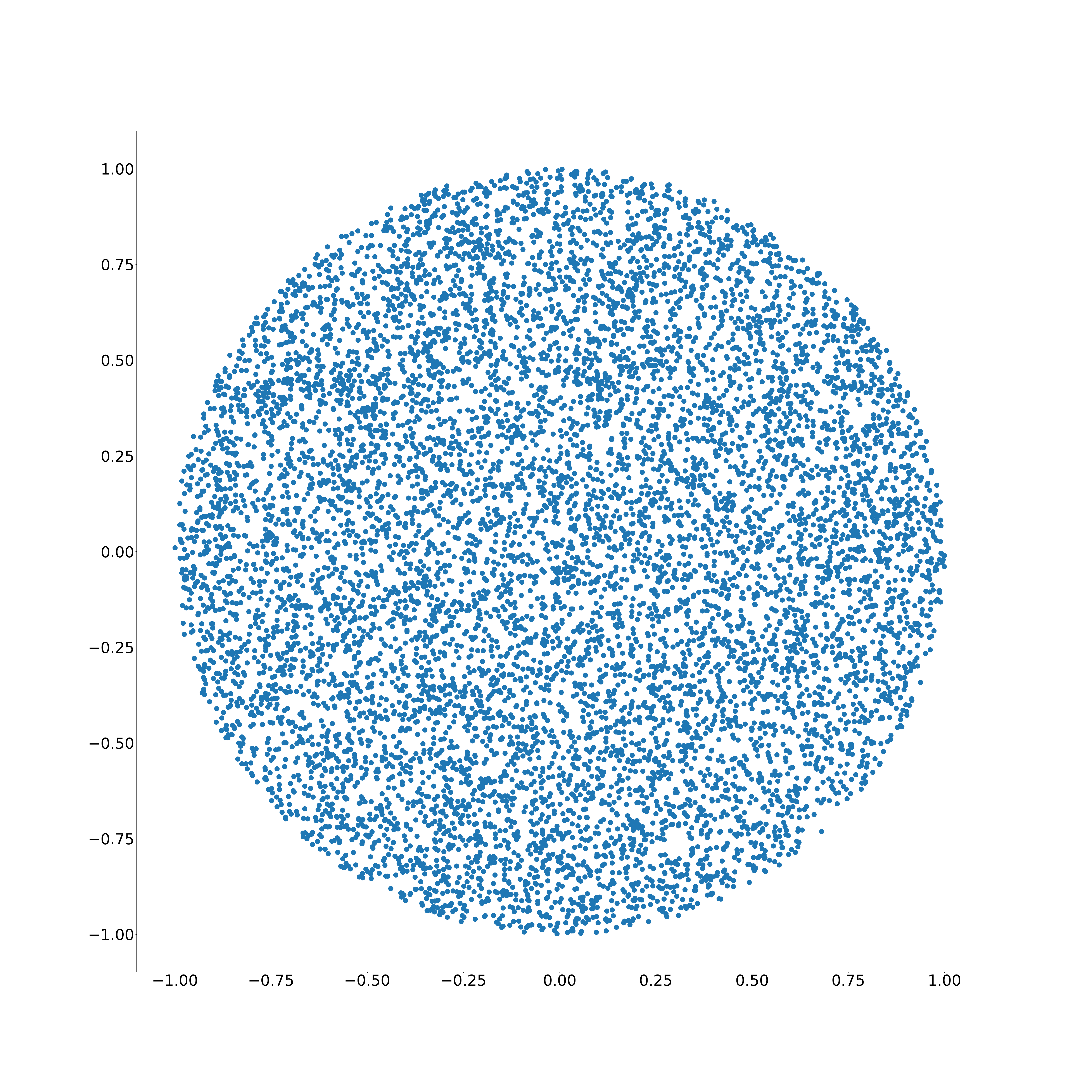
Damit erreichen wir eine Menge von gleichverteilten Punkten in einem Kreis, ohne Punkte verwerfen zu müssen.

$(r, \varphi) = (\sqrt{random()}, random() \cdot 2 \pi$)